Mẹo tính nhẩm thần tốc như thiên tài

Nếu dạo gần đây xem show trí tuệ University War siêu hot của Hàn Quốc thì có phải bạn đang trầm trồ vì độ nhanh khi các người chơi tính các phép tính dài ngoằng đúng không? Bạn sẽ tự hỏi là liệu mình có làm được như vậy hay không? Thật sự thì để thông minh được như vậy là cần cả một quá trình dài luyện tập cũng như trí tuệ thiên bẩm. Tuy nhiên, có một vài mẹo tính nhẩm sau có thể giúp bạn tính nhẩm siêu nhanh mà không cần dùng máy tính. Hãy cùng tìm hiểu nhé!

1. Chia nhỏ vấn đề

Đơn giản hóa những vấn đề phức tạp bằng cách chia nhỏ nó ra, thành những phần dễ quản lý hơn.

Ví dụ: 18 x 5 = (20 – 2) x 5 = 20 x 5 – 2 x 5 = 100 – 10 = 90.

2. Điều chỉnh số

Điều chỉnh các con số để dễ làm việc hơn, sau đó bù đắp cho việc điều chỉnh sau đó.

Ví dụ: 29 + 68 = (29 + 1) + (68 – 1) = 30 + 67 = 97.

3. Ghi nhớ bảng nhân

Biết bảng nhân tối thiểu 10×10 là vô cùng hữu ích và có thể tăng tốc độ tính toán của bạn một cách đáng kể. Nếu ngày xưa đi học thầy cô dạy bảng cửu chương từ 2 đến 9 thì bây giờ bạn có thể học thêm bảng 10, 11, 12,… Nó sẽ giúp bạn tính nhanh hơn nhiều trong một vài trường hợp.

4. Sử dụng mẫu và các mối quan hệ

Nhận biết các mẫu trong phép tính, chẳng hạn như thuộc tính phân phối (a (b + c) = ab + ac), để đơn giản hóa các phép tính.

Ví dụ: 14 x 5 = (10 + 4) x 5 = 10 x 5 + 4 x 5 = 70.

5. Bình phương số tận cùng bằng 5

Đối với bất kỳ số nào tận cùng bằng 5, bình phương của nó là số được hình thành bằng cách nhân số đứng đầu (trừ số 5 ở cuối ra) với số cao hơn 1 đơn vị và viết thêm 25.

Ví dụ:

• 25^2 = (2 x 3) 25 = 625.
• 115^2 = (11 x 12) 25 = 13225.

6. Nhân với 11

Để nhân một số có hai chữ số với 11, hãy cộng hai chữ số đó lại với nhau và đặt tổng vào giữa chúng. Nếu tổng lớn hơn 9 thì chuyển chữ số thừa sang trái.

Ví dụ:

• 34 x 11 = 3 (3+4) 4 = 374.
• 59 x 11 = 5 (5 + 9) 9 = 5 14 9 = (5 + 1) 4 9 = 649.

7. Nhân đôi và giảm một nửa

Đối với phép nhân, nếu một số chẵn, bạn có thể giảm một nửa số đó và nhân đôi số còn lại để tính toán dễ dàng hơn.

Ví dụ: 16 x 25 = (8 x 2) x 25 = 8 x (2 x 25) = 8 x 50 = 4 x 100 = 400.

8. Chia cho 5

Nhân 2 và chia cho 10 là một cách dễ dàng để chia một số cho 5.

Ví dụ: 115 / 5 = 115 x 2 /10 = 230 / 10 = 23.

9. Tính phép trừ với số bị trừ là 10^n

Để trừ một số lớn như 1.000 hoặc 10.000,…hãy trừ từng chữ số từ trái qua phải với 9 và chữ số cuối cùng với 10.

Ví dụ:

• 1000 – 467 = (9 – 4) (9 – 6) (10 – 7) = 533.
• 10000 – 4189 = (9 – 4) (9 – 1) (9 – 8) (10 – 9) = 5811.

10. Bình phương số gần 50

Hãy nhớ rằng 50^2 = 2500. Đối với các số gần 50, bạn có thể lấy 2500 cộng hoặc trừ với số chênh lệch nhân với 100, sau đó lại cộng thêm số chênh lệch bình phương. Nói chính xác thì nó áp dụng hằng đẳng thức 1 và 2 để nhẩm.

Ví dụ:

• 53^2, 53 so với 50 sẽ hơn 3 đơn vị, vậy số chênh lệch là +3.

Vậy 53^2 = 2500 + 3 x 100 + 3^2 = 2809.

Giải thích 1 chút: 53^2 = (50 + 3) ^2 = 50^2 + 2 x 50 x 3 + 3^2 = 2500 + 3 x 100 + 9 = 2809.

• 46^2, 46 so với 50 bé hơn 4 đơn vị, vậy số chênh lệch là -4.

Vậy 46^2 = 2500 – 4 x 100 + 4^2 = 2116.

11. Nhân với 9, 99, 999…

Để nhân với 9, bạn có thể nhân với 10 rồi trừ đi số ban đầu.

Ví dụ:

• 14 x 9 = 14 x 10 – 14 = 126.
• 23 x 99 = 23 x 100 – 23 = 2277.

12. Bình phương số gần 100

Áp dụng hằng đẳng thức như mẹo số 10.

Ví dụ: 98^2 = (100 – 2) ^2 = 100^2 – 2 x 100 x 2 + 2^2 = 10000 – 400 + 4 = 9604.

13. Nhân các số gần với 100

Sử dụng công thức (a – b) (a – c) = a^2 – ac – ab + bc, với a là 100.

Ví dụ: 98 x 97 = (100 – 2) x (100 – 3) = 100^2 – 3 x 100 – 2 x 100 + 3 x 2 = 9506.

14. Nhân 2 chữ số

Trường hợp 1: Với số hàng chục bằng nhau và số hàng đơn vị cộng lại bằng 10.

Ví dụ: 46 x 44 = ?

Ta lấy hàng chục nhân với số hơn nó 1 đơn vị, viết ra kết quả, sau đó lấy hàng đơn vị nhân với nhau, viết tiếp kết quả.

Để dễ hình dung thì bạn có thể nhìn ảnh sau:

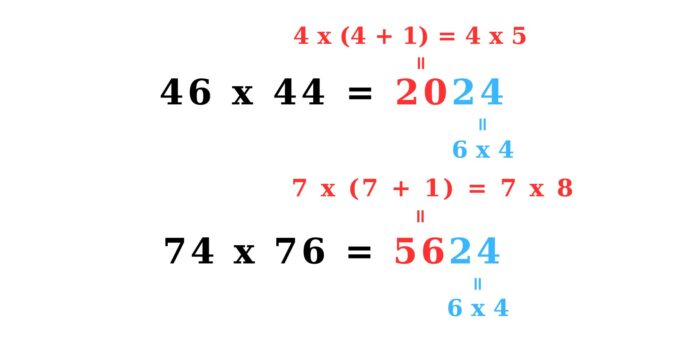
Trường hợp 2: Với hàng chục cộng lại bằng 10 và hàng đơn vị bằng nhau.

Ví dụ: 44 x 64 = ?

Ta lấy hàng chục nhân với nhau, sau đó cộng với hàng đơn vị, viết ra kết quả. Lấy hàng đơn vị nhân với nhau và viết tiếp kết quả có được.

Để dễ hình dung thì bạn có thể nhìn ảnh sau:

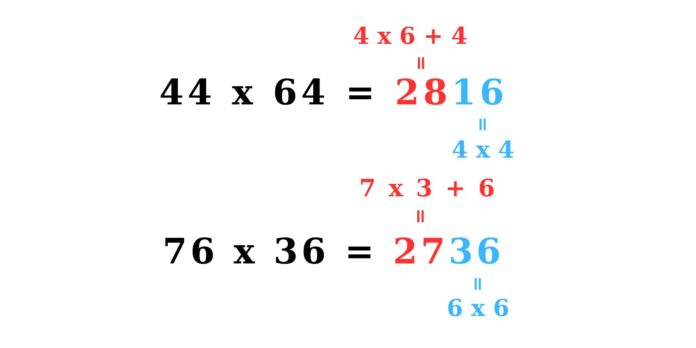
Kết luận

Việc luyện tập tính nhẩm là một kỹ năng giúp nâng cao khả năng toán học của chúng ta và cải thiện khả năng giải quyết vấn đề. Bằng việc áp dụng những mẹo đã được trình bày trong bài viết này, bạn có thể rèn luyện trí óc, tăng tốc độ tính toán và tự tin hơn với khả năng phân tích số học nhanh chóng và chính xác.

Cho dù bạn đang chia hóa đơn, tính lương hay chỉ đơn giản là muốn cải thiện năng lực nhận thức của mình, sức mạnh của những phép tính nhẩm là không thể phủ nhận.

Nhớ rằng, giống như bất kỳ kỹ năng nào, sự thành thạo trong việc tính nhẩm đến từ việc luyện tập và kiên nhẫn theo thời gian. Vậy nên, hãy tiếp tục đặt thử thách cho bản thân với các con số và bạn sẽ sớm nhận ra rằng việc từng tưởng chừng như khó khăn giờ đây trở nên vô cùng đơn giản.

Bạn có thể quan tâm:

• Học siêu đỉnh như thiên tài: Những phương pháp học tập hiệu quả mà bạn nên biết
• Luật giả định là gì? Nó khác gì với luật hấp dẫn?
• Laptop bị tê khi đang cắm sạc có nguy hiểm không? Nguyên nhân và cách khắc phục

Xem thêm

Review anime Attack on Titan: Hy sinh và Tự do

Attack on Titan, hay Shingeki no Kyojin, là một bộ anime lấy bối cảnh một thế giới hậu tận thế. Bấy giờ, phần ít nhân loại sống sót và phải trốn sau những bức tường cao lớn để bảo vệ họ khỏi những Titan hình người khổng lồ. Nhân vật chính Eren Yeager cùng với những người bạn là ...